一般相対性理論のためのリーマン幾何学

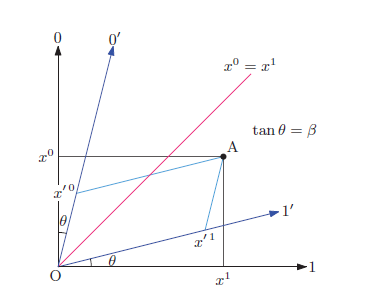
平坦な空間において, リーマン幾何学の記法を用い, リーマン幾何学の 数学に慣れていきます。その過程で, リーマン幾何学における 計量 (テンソル) の幾何学的意味などをつかんでいけるはずです。

• 一次変換の例として, 座標回転, ローレンツ変換を紹介する。
• アインシュタインの総和の規約で, 数式記述の労力を軽減。
• 行列式と余因子行列の関係。
• 斜交座標を例に, 計量についてのイメージを理解する。

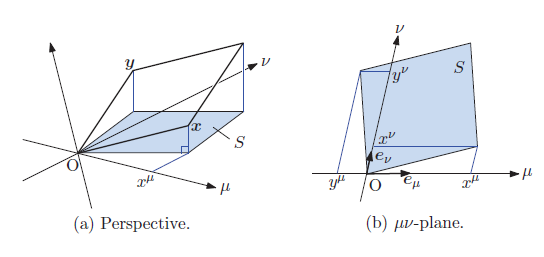
前章を発展させ, 曲がった空間を取り扱います。座標変換の観点で, スカラ, ベクトル, テンソルの意味を説明し, ベクトルテンソルには 共変成分と反変成分という2種類の成分の分け方があることに言及します。

• 曲がった空間での基本ベクトル (単位ベクトルではない)。
• スカラ, ベクトル, テンソルについて座標変換の観点で説明する。
• テンソルの対称性と反対称性。
• デュアルテンソル: 後に出てくる回転ベクトルにつながる。

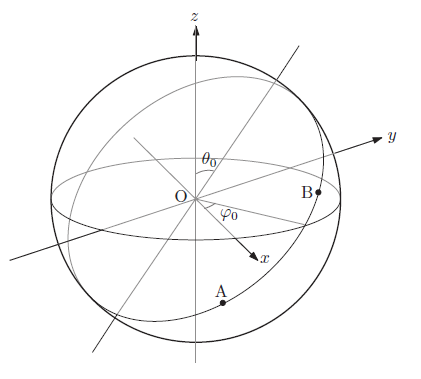
曲がった空間で2点を結ぶ最短経路は測地線と呼ばれます。 本章では, 変分法を用いて測地線を定式化します。 一般相対性理論では, 測地線が運動方程式に相当します。

• 曲がった空間での経路の長さを定式化する。
• 経路長を最短にする経路として, 変分法を用いて測地線を特定する。
• 測地線の方程式に含まれるクリストッフェル記号は基本ベクトルの 変化率である。
• 球面の測地線が大円コースであることを証明する。

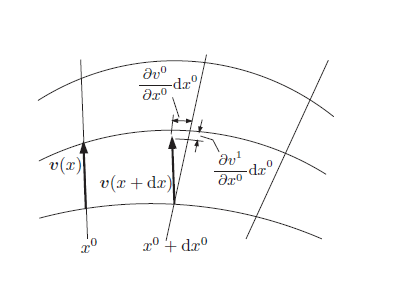
曲がった空間におけるベクトルの微分を取り扱います。 共変微分の観点でベクトルやテンソルの成分を微分すると, 単なる座標成分による微分だけでなく, クリストッフェル記号を伴う項を 追加する必要があります。その追加項は, 基本ベクトルが場所によって 異なるから発生します。

• ベクトルやテンソルの共変微分。基本ベクトルの変化率を考慮し, 共変微分の幾何学的意味を解説する。
• 計量テンソルの共変微分はゼロになる。
• 曲がった空間の勾配・発散・回転を定式化。
• ベクトル平行移動とは, 測地線に沿って移動したとき, 測地線とベクトルがなす角度を一定に保つことである。

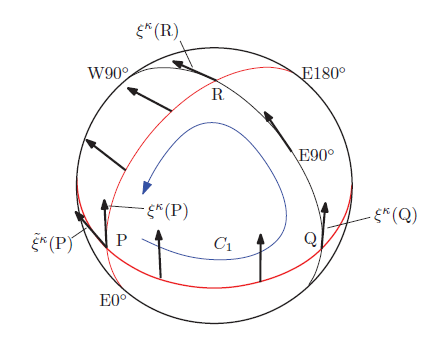
曲がった空間では, 周回軌道に沿ってベクトルを平行移動したとき, ベクトルの向きが変わってしまいます。その量を評価するには 曲率テンソルを利用します。曲率テンソルは, 計量テンソルの2階微分で 計算される4階のテンソルです。そのテンソルを縮約し, リッチのテンソル, スカラ曲率が定義できます。リッチのテンソルとスカラ曲率を組み合わせ, 一般相対性理論では重力場の方程式が形成されます。

• 曲率テンソルは, 空間の湾曲を表す量である。
• 曲率テンソルは多くの対称性をもち, 独立成分が希薄である。
• リッチテンソルに関するビアンキの恒等式は, 物理学における保存則に対応する。
• アインシュタインテンソルだけでは定常な宇宙が表現できない。 だから宇宙項を追加する?!
• 平坦な空間では曲率テンソルがゼロになる。

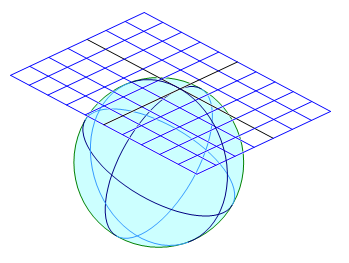
曲がった空間のいかなる場所でも, 局所的にユークリッド空間と みなすことができる。その意味で, ある基準の場所に ユークリッド空間が接するように定めた座標系は標準座標系と呼ばれる。

• 測地線を座標軸に設定し, 標準座標系を得る。
• 標準座標系では, 基準位置において, クリストッフェル記号がゼロになる。
• 標準座標系では, 計量テンソルが, 基準位置からの距離に伴い単位行列からの ずれが大きくなる。その変化の大きさは曲率テンソルに比例する。
• 標準座標系において, リッチテンソルは体積歪みの大きさを与える。

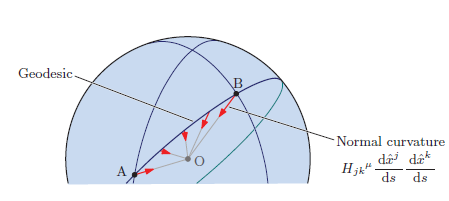
一般のn次元空間の中に, 座標の数を限定して少ない次数で表現できる 空間が部分空間です。例えば, 3次元空間中の球面が部分空間の例です。 地球での位置特定は緯度と経度を使います。つまり, 2次元に限定した 部分空間です。部分空間の概念を使うと, 外の空間から測地線を見ると どう見えるか? 曲がった空間にいる本人には曲がっていることが気付かない など, いろんな視点で曲がった空間が見えてきます。

• 部分空間の計量、クリストッフェル記号の関係を調べる。
• 注目する方向を変えて曲率を平均する。
• 部分空間での測地線は、法曲率しか存在しない。球面の測地線は 大円コース以外にはありえない。
• ガウス曲率に相当するスカラ量 (リーマン曲率) 導出。